200以上 場合の数 求め方 418449-場合の数 求め方

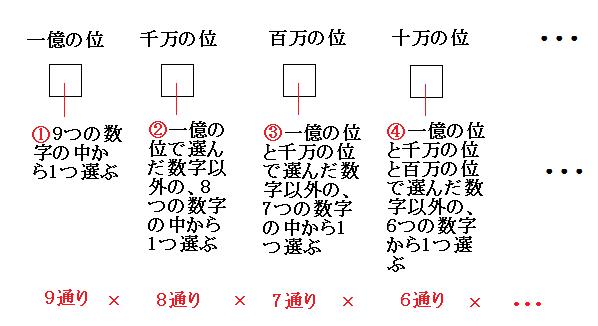
N桁の数を作る場合の数の求め方 条件が厳しい所から決めて行く
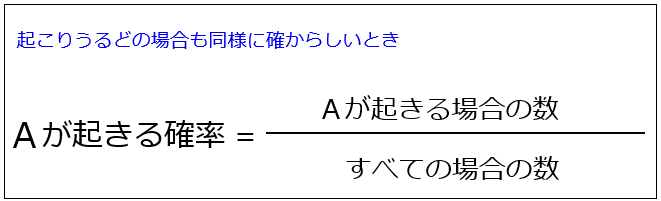
場合の数の勉強方法! 組み合わせと順列の解き方と勉強のコツ! 算数、数学と言っても、たいていの分野は公式を暗記することによってある程度を習得することができます。 「公式を暗記すること」と、「公式を問題に当てはめること」が比較①起こりうる全ての場合の数の集合を U、 確率を求めたい場合の数の集合を a とすると a の起こる確率 は次のように表せます。 ② 確率を求めるにあたって、 場合の数を数えるとき、抜けが無いようにするため、組合せで考えて場合を書き出し(昇順または降順で書き出す)、順列の計算を
場合の数 求め方
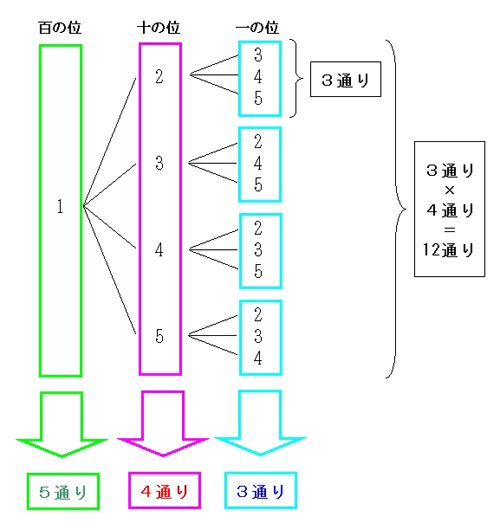
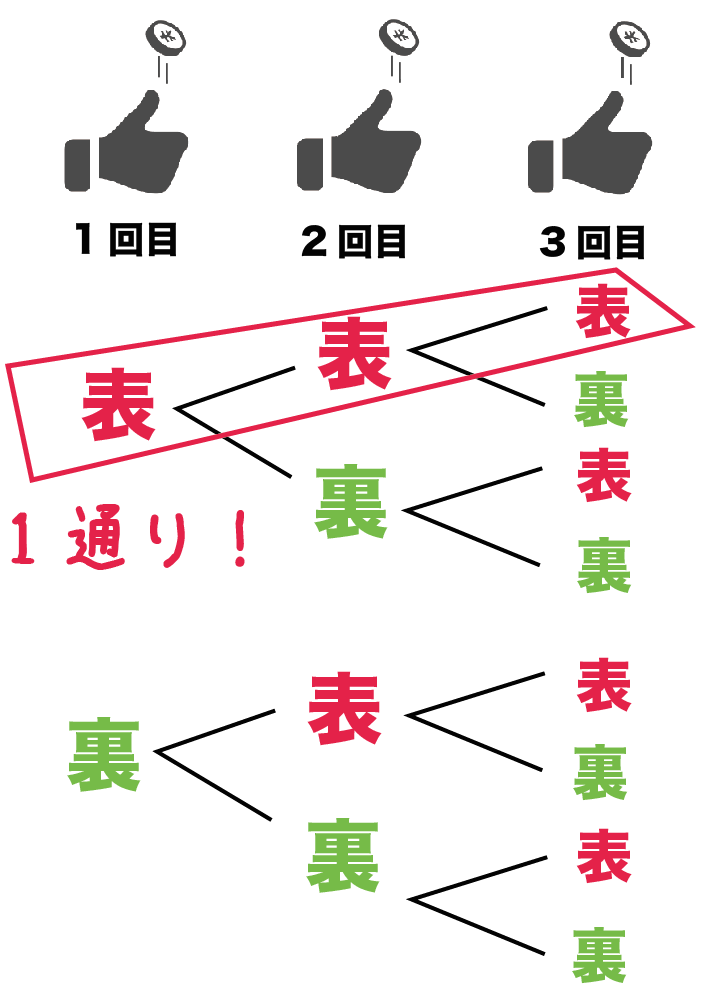
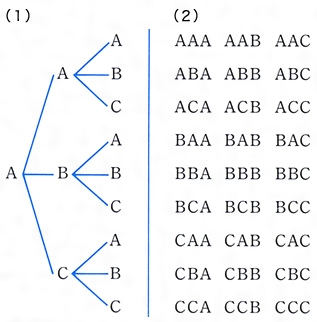
場合の数 求め方-ここまでの場合の数は式で書くと \(3\times 2\) ですね。その次は残りの1人だけなのでパターンは1通りです。 \(3\times 2\times 1\) ですよね。これは樹形図でいうと のように理解できます。実はこれが順列の考え方です。つまり 樹形図の考え方を式で計算したものたとえば√14の近似値を求める場合、 √14 = √2×√7 ≒ 141×264 = 2<√a<3をみたす自然数aの求め方 問題2<√a<3をみたす自然数aを求めよ。 解説 ルートがあるから大きさがわかりにくい。ならば外してしまえ!という考え方をします。 2<√a<3 正の値を2乗しても不等式の大小関係は

小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生
Step3)異なるr個を並べる(順位づけをする)場合の数の求め方 問い)40人に順番をつける方法は何通りか。 これを倍率で考えると、1番になる人の倍率は、 である。次の残り39人から2番になる人の倍率を考えると であるから以下同様に求めていくと、その場合の数は、 40×39×38××3×2×1=40! とこのことから場合の数と確率は非常に似ていることがわかります. そのため 確率を極めたければ,場合の数を極めるべし! では場合の数について見ていきましょう. 場合の数はどうやって求めるの? 条件に合うものを 書きだすのも1つの手 ですこれに対して、順列という並べ方の数(Permutation)を表す nPr という記号もあるのですが、そちらは上は違う並べ方と考えます。nCr と nPr は、とても似ているので混乱しないようにしましょう。 関連記事:5分で分かる!確率統計「nPr」順列の計算方法 nCr の計算方法 詳細な公式や証明は、高校
正の数と負の数 22 文字と式(中学) 19 一次方程式 23 比例と反比例(中学) 16 平面図形(中学) 33 高校数学全般 6 実数 32 展開と因数分解 28 集合と命題 38 一次不等式 18 二次関数 101 三角比 77 データの分析 45 場合の数 53 確率 75 整数 平面図形 26 空間図形 9 式の計算 30 二項定理 14 等式と不順列か?組み合わせか?の判断テクニック ①順列 異なるn個の中から k 個を 順番をつけて並べる 場合の並べ方は n P k で表され、順列の公式から求められますデータの数が偶数個の場合 例えば、10個のデータ \(1,2,3,4,5,6,7,8,9,10\) の第3四分位数を求める場合、先ほどの求め方だと \(8\) になるはずですが、Quartile関数だと \(775\) という答えが返ってきます。 (中央値は同じ答え) このExcelの厳密な四分位数(Quartile関数)の求め方はさきほどのヒンジと
場合の数 求め方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
「場合の数 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「場合の数 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「場合の数 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「場合の数 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
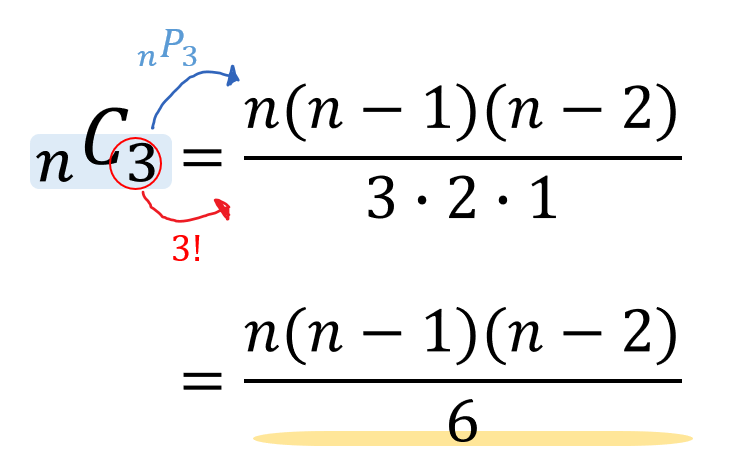 |  | |
 |  |  |
「場合の数 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「場合の数 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「場合の数 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「場合の数 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「場合の数 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
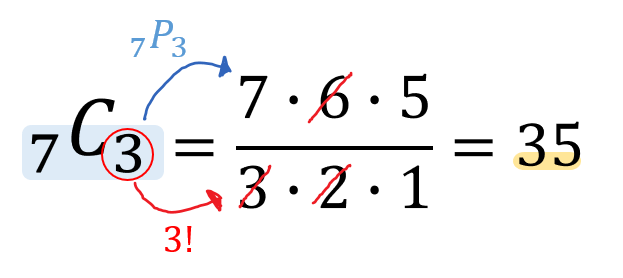 |  |  |
「場合の数 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「場合の数 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
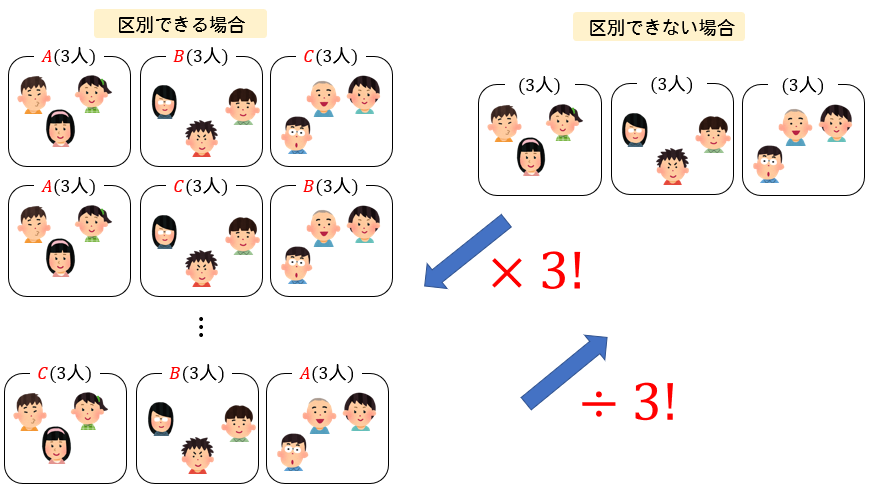
確率を求める方法の1つは,場合の数を求めて割り算することです。その方法を見ていきましょう。考え方を理解しよう!!あうるさん さいころの目は全部で何通りですか? 1~6まで目があるから6通りだね。 あうるさん それでは,さいころを1回振ってよって、(3)では、(2)で求めた場合の数を同じ分け方となる数(A、B、Cの順列の数)で割っているのです。 アドバイス いくつかのものを何組かに分ける方法の数を求めるには、組合せの考え方を1組ずつ順番に使って求めていきます。 その際、区別できない組があるときには、 step1 組に区別が
Incoming Term: 場合の数 求め方,
コメント
コメントを投稿